Page 49 - 捷運技術 第39期

捷運技術半年刊 第39期 97年8月 43

表中係以預測模式採總量位準為例，故由振動轉換為二次噪音則視軌道頻率採總量直接
轉換。
預測模式將以基本關係曲線圖為基礎，再依據表6就影響因子進行修正，其中包括評估

適切的減振措施。
2. 傳遞動性預測模式【Nelson，1988】【FTA，1995】【FRA，1998】
傳遞動性（Transfer Mobility, TM）的定義為單位負荷作用下所產生之振動，經由軌道

結構或土層的傳遞衰減，而在受體位置所量得之速度振動位準。傳遞動性預測模式是由美國
WIA公司（Wilson, Ihrig and Associates, Inc.）在1980年代所建立，其是以鑽孔試驗（Borehole
Test）或落錘試驗為基礎，用來預測輪軌振動經由結構、地層衰減後傳至受體的振動與二次
噪音位準，一般係以各頻帶位準表示。相關公式如下：
LV＝FDL＋TMline＋Cbuild （15） 20.0

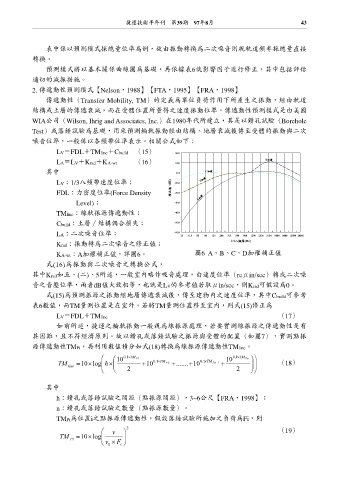
LA＝LV＋Krad＋KA-wt （16） 10.0 Dу៾
其中 0.0 Cу៾
LV：1/3八頻帶速度位準； (dB) -10.0 Bу៾

FDL： 力密度位準(Force Density ံ҅ॶ -20.0
Level)； -30.0 Aу៾
TMline：線狀振源傳遞動性； -40.0
Cbuild：土層／結構偶合損失； -50.0
LA：二次噪音位準； -60.0 20 31.5 50 80 125 200 315 500 800 1250 2000 3150 5000 8000 12500 20000
1/3Ζᓎ஥(Hz)
Krad：振動轉為二次噪音之修正值；
KA-wt：A加權補正值，詳圖6。 圖6 A、B、C、D加權補正值
式(16)為振動與二次噪音之轉換公式，

其中Krad如五、(二)、5所述，一般室內略作吸音處理，由速度位準（reμin/sec）轉成二次噪
音之音壓位準，兩者dB值大致相等，也就是LV的參考值若取μin/sec，則Krad可假設為0。
式(15)為預測振源之振動經地層傳遞衰減後，傳至建物內之速度位準，其中Cbuild可參考
表6數值，而TM量測位置是在室外。若將TM量測位置移至室內，則式(15)修正為

LV＝FDL＋TMline （17）
如前所述，捷運之輪軌振動一般視為線振源處理，若要實測線振源之傳遞動性是有
其困難，且不符經濟原則。故以鑽孔或落錘試驗之振源與受體的配置（如圖7），實測點振
源傳遞動性TMPi，再利用數值積分如式(18)轉換為線振源傳遞動性TMline。

§ §10 u 1 . 0 TM P 1 10 u 1 . 0 TM Pn · ·
¨ u
TM line 10 ulog h ¨ 10 u 1 . 0 TM P 2 ....... 10 u 1 . 0 TM Pn 1 ¸ ¸ ¸ ¸ （18）
¨
¨
© © 2 2 ¹ ¹
其中
h：鑽孔或落錘試驗之間距（點振源間距），3~6公尺【FRA，1998】；

n：鑽孔或落錘試驗之數量（點振源數量）。
TMPi為位置i之點振源傳遞動性，假設落錘試驗所施加之負荷為Fi，則

§ v · 2 （19）
TM Pi 10u log¨ ¸
¨
¸
© v 0 u F i ¹