Page 51 - 捷運技術 第39期

捷運技術半年刊 第39期 97年8月 45

物等等，不同介質在振動傳遞上會有偶合損失，相同介質因均質性問題，其振動衰減亦未必
處處相同。理論上，由振源至受體之間的傳播路徑，可視介質變異性及不同介質特性而分別
建立個別TMi，則整體TM為傳播路徑上所有個別TMi的總合，即

TM＝ΣTMi （23）
因此，振動預測模式不一定要建立在振源位置，亦可取距離軌道中心線適切位置作為預
測模式之基準，例如臺北捷運FE-31振動預測模式就選定距離軌道中心線10公尺為參考點，

屆時再以前述各項修正因子對振動位準進行修正。
為綜合述說明，茲從文獻中節錄完整實測數據(圖9)，以供讀者驗證參考。【Saurenman,
2006】

RMS Vlb. Veloclty Level, VdB re 1 μin/sec Line Source Transfer Mobility dB re 1 lb/(μin/sec)/sqrt(ft)

1/3 Octave Band Center Frequency, Hz
1/3 Octave Band Center Frequency, Hz
Hayward Test Track 28 ft 57 ft. 107 ft. Hayward Test Track 28 ft 57 ft. 107 ft.
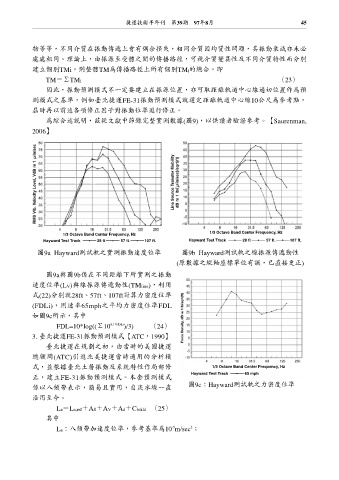
圖9a Hayward測試軌之實測振動速度位準 圖9b Hayward測試軌之線振源傳遞動性
(原數據之縱軸座標單位有誤，已直接更正)

圖9a與圖9b係在不同距離下所實測之振動
速度位準(LV)與線振源傳遞動性(TMline)，利用
式(22)分別就28ft、57ft、107ft計算力密度位準
(FDLi)，則速率65mph之平均力密度位準FDL
如圖9c所示，其中

FDL=10*log((Σ10 0.1*FDLi )/3) （24）
3. 臺北捷運FE-31振動預測模式【ATC，1990】
臺北捷運在規劃之初，由當時的美國捷運

總顧問(ATC)引進北美捷運當時通用的分析模
式，並根據臺北土層振動及系統特性作局部修 1/3 Octave Band Center Frequency, Hz
Hayward Test Track 65 mph
正，建立FE-31振動預測模式。本套預測模式
圖9c：Hayward測試軌之力密度位準
係以八頻帶表示，簡易且實用，自淡水線一直
沿用至今。

La＝La,ref＋AS＋AV＋Ad＋Cbuild （25）
其中
2
La： 八頻帶加速度位準，參考基準為10 m/sec ；
-5