Page 62 - 捷運工程叢書 精進版 － 21 捷運電聯車實務

個之自由度（Dof）。為了簡化問題，首先考慮一個轉向架在一維空間之運動方程式（Equation
臺北市政府捷運工程局
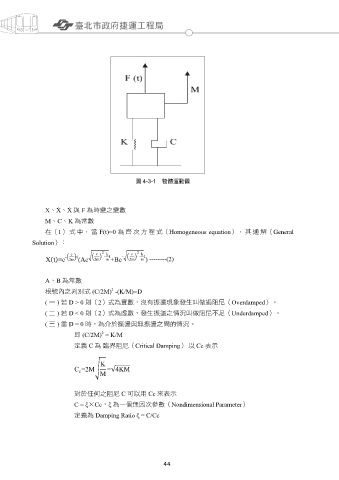
of Motion），如圖 4-3-1 所示。
個之自由度（Dof）。為了簡化問題，首先考慮一個轉向架在一維空間之運動方程式（Equation
MX(t)+C(t)+KX(t)=F(t)---------(1)
̈
̇
of Motion），如圖 4-3-1 所示。
M : 單一轉向架重量（Mass Of One Bogie）
MX(t)+C(t)+KX(t)=F(t)---------(1)
̈
̇
C : 阻尼（Damping）
M : 單一轉向架重量（Mass Of One Bogie）
K : 彈簧勁度（Spring Stiffness）
C : 阻尼（Damping）
F : 施加力（Applied Force）
K : 彈簧勁度（Spring Stiffness）
X : 位移（Displacement Of Mass）
F : 施加力（Applied Force）
: 速度（Velocity Of Mass）
̇
X : 位移（Displacement Of Mass）
: 加速度（Acceleration Of Mass）
̈
: 速度（Velocity Of Mass）
̇

: 加速度（Acceleration Of Mass）
̈

圖 4-3-1 物體運動圖

X、Ẋ、Ẋ 與 F 為時變之變數 圖 4-3-1 物體運動圖
X、 、 與 F 為時變之變數
M、C、K 為常數
̇
̇
圖 4-3-1 物體運動圖
在（1） 式 中， 當 F(t)=0 為 齊 次 方 程 式（Homogeneous equation）， 其 通 解（General
M、C、K 為常數
X、 、 與 F 為時變之變數
̇
̇
在（1）式中，當 F(t)=0 為齊次方程式（Homogeneous equation），其通解（General Solution）：
Solution）：
M、C、K 為常數
2
2
k
c
c
k
在（1）式中，當 F(t)=0 為齊次方程式（Homogeneous equation），其通解（General Solution）：
c
) - t
)t
) - t
+Be
2m (Ae
--------(2)
X(t)=e
√ (
- √ (
-(
2m
2m
m
)--------(2)
m
c c 2 k c 2 k
)t
X(t)=e
A、B 為常數 √ ( 2m ) - t +Be - √ ( 2m ) - t )--------(2)
2m (Ae
-(
m
m
A、B 為常數 2
根號內之判別式 (C/2M) -(K/M)=D
A、B 為常數
2
根號內之判別式 (C/2M) -(K/M)=D
(一) 若 D > 0 則（2）式為實數，沒有振盪現象發生叫做過阻尼（Overdamped）。
2
根號內之判別式 (C/2M) -(K/M)=D
( 一 ) 若 D > 0 則（2）式為實數，沒有振盪現象發生叫做過阻尼（Overdamped）。
(二) 若 D < 0 則（2）式為虛數，發生振盪之情況叫做阻尼不足（Underdamped）。
(一) 若 D > 0 則（2）式為實數，沒有振盪現象發生叫做過阻尼（Overdamped）。
(三) 當 D = 0 時，為介於振盪與無振盪之間的情況。
( 二 ) 若 D < 0 則（2）式為虛數，發生振盪之情況叫做阻尼不足（Underdamped）。
(二) 若 D < 0 則（2）式為虛數，發生振盪之情況叫做阻尼不足（Underdamped）。
2
即(C/2M) = K/M
( 三 ) 當 D = 0 時，為介於振盪與無振盪之間的情況。
(三) 當 D = 0 時，為介於振盪與無振盪之間的情況。
定義 C 為 臨界阻尼（Critical Damping） 以 Cc 表示
2
即 (C/2M) = K/M
2
即(C/2M) = K/M
定義 C 為 臨界阻尼（Critical Damping） 以 Cc 表示
定義 C 為 臨界阻尼（Critical Damping） 以 Cc 表示

= 2 √ = √4

K
C =2M√ =√4KM
c
M
對於任何之阻尼 C 可以用 Cc 來表示
C = ξ×Cc，ξ 為一個無因次參數（Nondimensional Parameter）
對於任何之阻尼 C 可以用 Cc 來表示
對於任何之阻尼 C 可以用 Cc 來表示
定義為 Damping Ratio ξ = C/Cc
C = ξ×Cc，ξ 為一個無因次參數（Nondimensional Parameter）
C = ξ×Cc，ξ 為一個無因次參數（Nondimensional Parameter）
依據 ξ 之數值可分下列三個情況來討論：
定義為 Damping Ratio ξ = C/Cc
定義為 Damping Ratio ξ = C/Cc 42
依據 ξ 之數值可分下列三個情況來討論：
42

44 45