Page 66 - 捷運工程叢書 精進版 － 14 捷運工程大區域降水施工實務

臺北市政府捷運工程局

4.1.3.2 Cooper-Jacob 直線法（時間─洩降半對數圖解法）

本法演自 Theis 方程式，兩者適用相同之理論假設條件。唯 Cooper-Jacob 直線法尚必須
符合 u ≦ 0.05 之條件。Cooper & Jacob 將 Theis 方程式簡化為

（4.1.3）

式中
s：水位洩降量
r：觀測井與抽水井距離

在同一含水層中之固定觀測點，T、S 和 r 為固定值，因此 s 隨 logt 變化。在以 s 為 Y 軸，
logt 為 X 軸的半對數圖中，符合式（4.1.3）條件的洩降曲線將成一直線。若△ s 為每一個時
間對數 cycle 的水位洩降量（直線斜率），T 值可由下式求得

（4.1.4）

S 值則可由直線在零洩降時與時間軸之截點（t ）求得
0
（4.1.5）

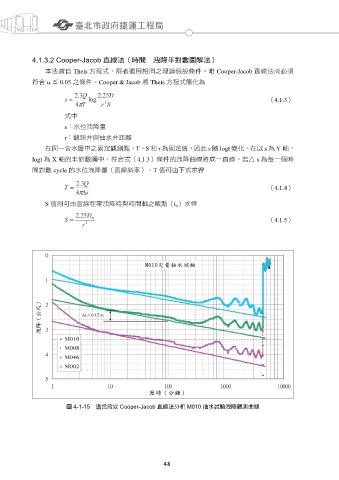
圖 4-1-15 道岔段以 Cooper-Jacob 直線法分析 M010 抽水試驗洩降觀測曲線

48 49